Goedel-Prover

A New Frontier in Open-source Automated Theorem Proving

Yong Lin*1 Shange Tang*1 Bohan Lyu2 Jiayun Wu2
Hongzhou Lin3 Kaiyu Yang4 Jia Li5 Mengzhou Xia1
Danqi Chen1 Sanjeev Arora1 Chi Jin1

1Princeton Language and Intelligence, Princeton University

2Tsinghua University, 3Amazon, 4Meta FAIR, 5 Numina

arXiv πŸ€— HuggingFace Code

Introduction

We introduce Goedel-Prover, an open-source large language model (LLM) that achieves the state-of-the-art (SOTA) performance in automated formal proof generation for mathematical problems. The key challenge in this field is the scarcity of formalized math statements and proofs, which we tackle in the following ways. We train statement formalizers to translate the natural language math problems from Numina into formal language (Lean 4), creating a dataset of 1.64 million formal statements. LLMs are used to check that the formal statements accurately preserve the content of the original natural language problems. We then iteratively build a large dataset of formal proofs by training a series of provers. Each prover succeeds in proving many statements that the previous ones could not, and these new proofs are added to the training set for the next prover. The final prover outperforms all existing open-source models in whole-proof generation. On the miniF2F benchmark, it achieves a 57.6% success rate (Pass@32), exceeding the previous best open-source model by 7.6%. On PutnamBench, Goedel-Prover successfully solves 7 problems (Pass@512), ranking first on the leaderboard. Furthermore, it generates 29.7K formal proofs for Lean Workbook problems, nearly doubling the 15.7K produced by earlier works.

Key Achievements

Improving

+7.6%

over previous SOTA on miniF2F Pass@32

Ranking

1st

on the PutnamBench Leaderboard

Solving

1.9X

total problems compared to prior works on Lean-workbook

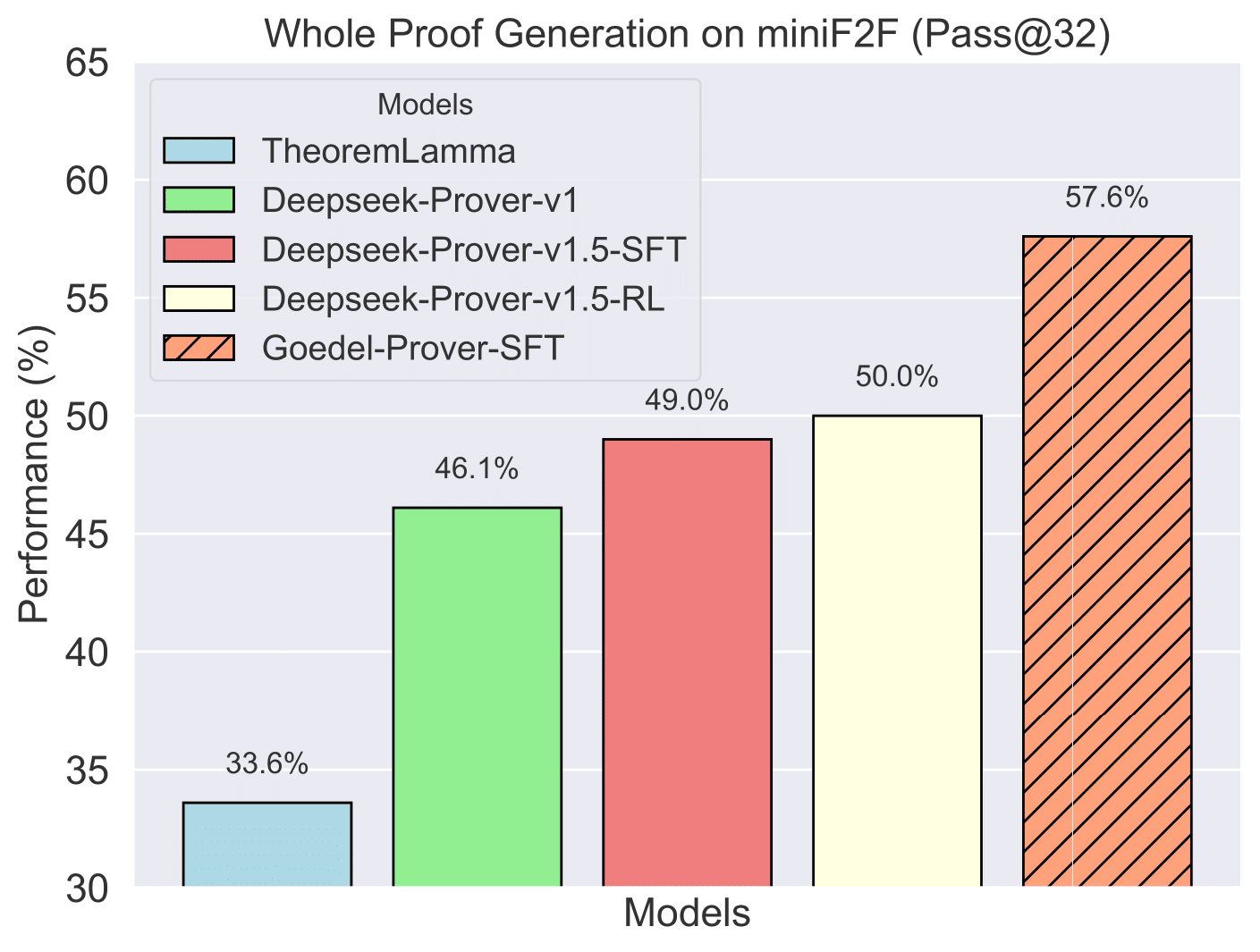
miniF2F Performance
Performance of Pass@32 for full proof generation on miniF2F
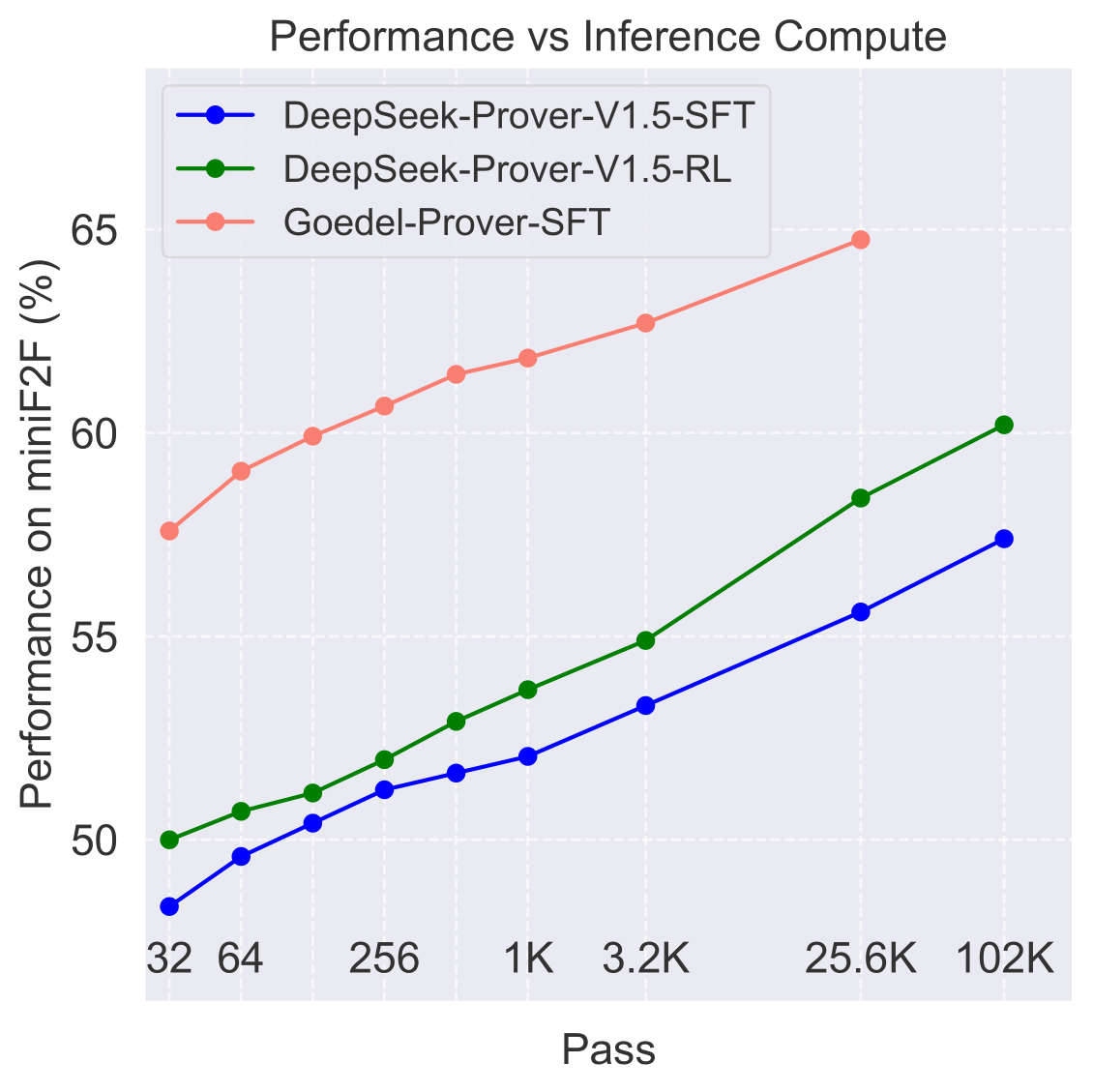
Inference Scale Performance
Comparison across different inference budgets
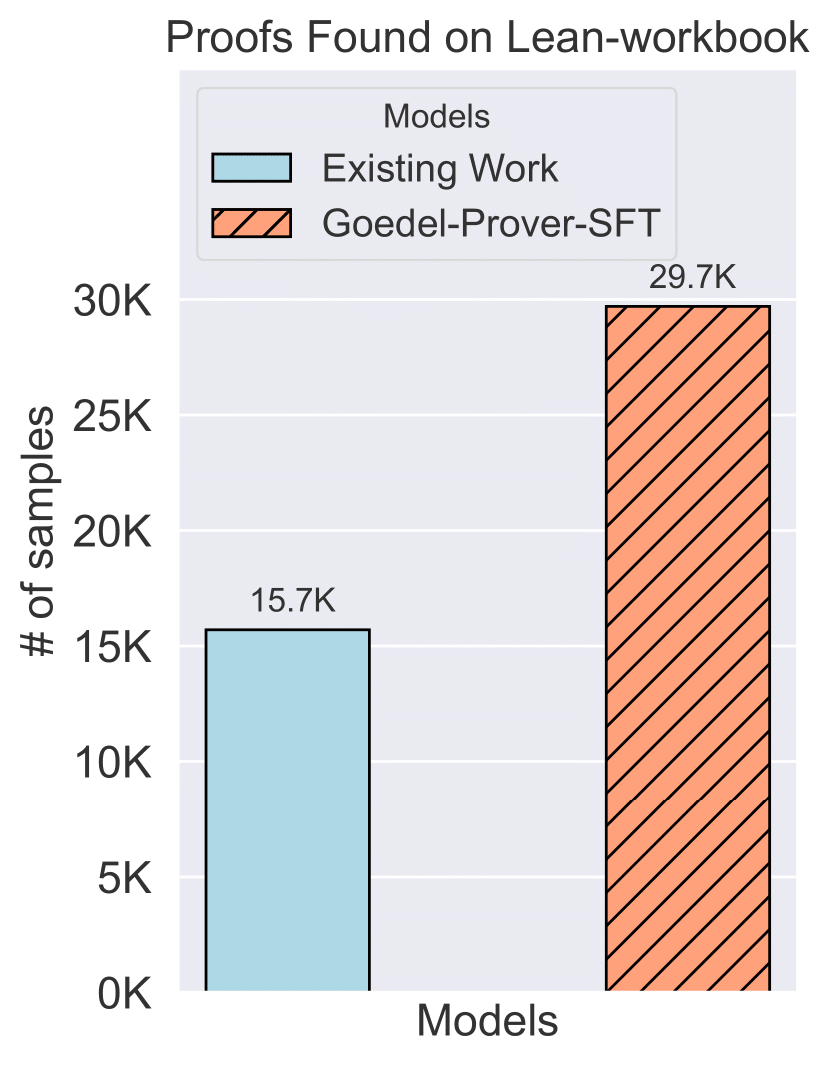
Leanworkbook Proofs
Number of problems solved in Lean-workbook

The Pass@N metric indicates that we generate N proofs for a single problem; if any one of these N proofs successfully solves the problem, it is considered solved. (Left): The performance of Pass@32 for full proof generation on miniF2F. Due to limited compute, we compare with DeepSeek-Prover-v1.5 on the Pass@32 metric. (Middle): This sub-figure presents a comparison of Goedel-Prover-SFT and Deepseek-Prover-v1.5 in terms of miniF2F performance across different inference budgets, ranging from Pass@32, 64, 128, ..., 4 Γ— 6400, to 16 Γ— 6400. (Right): The number of problems solved in Lean-workbook by Goedel-Prover-SFT compared to prior works. InternLM2.5-Step-Prover and InternLM-Math-Plus collectively solve and open-source 15.7K samples, while we solve and open-source 29.7K samples.

Methodology

Large-scale data synthesis and iterative training

Statement Formalization
Train two formalizers to formalize the statements.
  • Formalizer A: Trained on Lean workbook pairs
  • Formalizer B: Trained on 170K Claude-formalized statements
  • Each problem receives multiple formalizations

Detailed Process

We train two distinct formalizers to enhance statement diversity:

Formalizer A: Trained using Qwen2.5-Coder-32B on natural language and formal language pairs from Lean workbook.

Formalizer B: Trained on 170K statements formalized by Claude-sonnet-3.5 and syntactically verified by Lean compiler.

Training completed in under 24 hours using 8 H100 GPUs. Each problem receives 16 total formalizations (8 from each formalizer).

Quality Assessment
Assess and filter the formalized statements.
  • CC Test: Using LEAN compiler to verify syntax
  • FC Test: Using LLM as judge to verify accuracy and completeness

Compiling Correctness (CC) Test

  • Ensures formalized statements follow Lean syntax
  • Must successfully compile with placeholder ":= by sorry"

Faithfulness and Completeness (FC) Test

  • Evaluates accuracy of problem translation
  • Uses Qwen2.5-72B-Instruct for assessment
  • Generates 4 independent judgments per statement
  • Statements below 0.5 FC score are filtered out
Expert Iteration
Perform expert iteration on the formalized statements.
  1. Generate 16 proof candidates per statement
  2. Verify correctness
  3. Collect verified proofs
  4. Train new model and repeat process

Training Process

  • Uses DeepSeek-Prover-V1.5-RL for initial proof generation
  • Generates 16 proofs per problem
  • Compiles proofs to verify correctness
  • Retains one correct proof per statement
  • Trains new model (Prover-Iter-k) based on Deepseek-Prover-v1-Base with collected proofs
  • Iteratively improves through multiple training cycles
Data Scale
Statistics of the data scale.
  • 928K informal statements processed
  • 1.64M formalized statements
  • 140K Leanworkbook statements
  • Total: 1.78M formal statements

Data Sources

  • 860K problems from Numina datasets
  • 68K private collection from Art of Problem Solving (AOPS)
  • 140K statements from Leanworkbook and Leanworkbook-plus

Formalization Results

  • 760K problems with dual formalizations (both Formalizer A and B)
  • 123K problems with single formalization
  • Comprehensive coverage across different mathematical domains

Experimental Results

Benchmarks

Following previous works, we primarily use miniF2F as our main evaluation benchmark. Additionally, we track performance on ProofNet, Lean-workbook, and FormalNumina. Lean-workbook contains 140K statements in total. FormalNumina is a private test set created by formalizing a randomly sampled collection of 250 problems from Numina. The benchmarks represent a diverse range of mathematical problems, from high-school level to undergraduate mathematics.

Main Results

Table 2: Full Proof Generation Performance on miniF2F

Model Pass Performance
TheoremLamma 128 33.6%
Deepseek-Prover-v1 32 46.1% Β± 0.5%
Deepseek-Prover-v1.5-SFT 32 48.2% Β± 0.6%
Deepseek-Prover-v1.5-RL 32 50.0% Β± 0.5%
Goedel-Prover-SFT 32 57.6% Β± 0.7%
Deepseek-Prover-v1.5-SFT 3200 53.3%
Deepseek-Prover-v1.5-RL 3200 54.9%
Goedel-Prover-SFT 3200 62.7%
Deepseek-Prover-v1.5-SFT 4Γ—6400 55.8%
Deepseek-Prover-v1.5-RL 4Γ—6400 58.5%
Goedel-Prover-SFT 4Γ—6400 64.7%

Our Goedel-Prover-SFT achieves state-of-the-art performance on miniF2F, surpassing previous models by significant margins. The model shows consistent improvement across different computational budgets, achieving 57.6% at Pass@32, 62.7% at Pass@3200, and 64.7% at Pass@4Γ—6400.

Table 3: Performance Comparison Across Different Datasets

Model miniF2F ProofNet FormalNumina Lean-workbook
Deepseek-Prover-v1.5-RL 50.0% 16.0% 54.0% 14.7%
Goedel-Prover-SFT 57.6% (+7.6) 15.2% (-0.8) 61.2% (+7.2) 21.2% (+6.5)

The model demonstrates strong performance across multiple datasets, with notable improvements in miniF2F, FormalNumina, and Lean-workbook benchmarks. While performance on ProofNet shows a slight decrease, the overall average performance shows a significant improvement of 5.4 percentage points.

Table 4: Number of Problems Solved on PutnamBench (out of 644)

Ranking Model Type Num-solved Compute (Pass)
1 Goedel-Prover-SFT ♦ Whole Proof Generation 7 512
2 ABEL Tree Search Method 7 596
3 Goedel-Prover-SFT ♦ Whole Proof Generation 6 32
3 InternLM2.5-StepProver ♦ Tree Search Method 6 2Γ—32Γ—600
5 InternLM 7B Whole Proof Generation 4 4096
6 GPT-4o Whole Proof Generation 1 10
7 COPRA (GPT-4o) ♦ Whole Proof Generation 1 1
8 ReProver w/ retrieval ♦ Tree Search Method 0 1
9 ReProver w/o retrieval ♦ Tree Search Method 0 1

On the challenging PutnamBench dataset, Goedel-Prover-SFT achieves new state-of-the-art performance, solving 7 out of 644 problems with Pass@512, ranking the first place at the Putnam Leaderboard. ♦ indicates a open-source model.

Iterative Training Details

Given a set of formalized statements, we start by employing DeepSeek-Prover-V1.5-RL to generate 16 proofs for each problem. We evaluate these proofs and retain one valid proof per statement. Using this curated collection, we conduct supervised fine-tuning (SFT) on DeepSeek-Prover-V1.5-Base, resulting in Prover-Iter-1. This iterative process continues, with each version, Prover-Iter-k, generating new answers and training the model for subsequent iterations. Importantly, Prover-Iter-k is trained based on the proofs collected from the previous iteration, Prover-Iter-(k-1). Additionally, we gradually increase the number of statements throughout the iterative training process. Starting from Iteration 6, we also incorporate Mathlib into the training data. The details of the data statistics for each iteration are presented in the table below.

Table 6: Iterative Training Details

Iteration Statements Training Data
Lean-workbook Formalized Statements Lean-workbook Solved Formalized Proofs Mathlib
Iter-0 140K 0 20.6K 0 0
Iter-1 140K 140K 20.6K 72.4K 0
Iter-2 140K 270K 23.0K 128.7K 0
Iter-3 140K 270K 24.4K 161.2K 0
Iter-4 140K 882K 25.4K 425.8K 0
Iter-5 140K 882K 27.0K 436.5K 0
Iter-6 140K 882K 27.8K 443.2K 104K
Iter-7 140K 1.64M 28.8K 887.7K 104K
Iter-8 140K 1.64M 29.7K 915.7K 104K
Iter-9 140K 1.64M 30.3K 928.2K 104K

The model's performance across four datasets during iterative training is shown below.

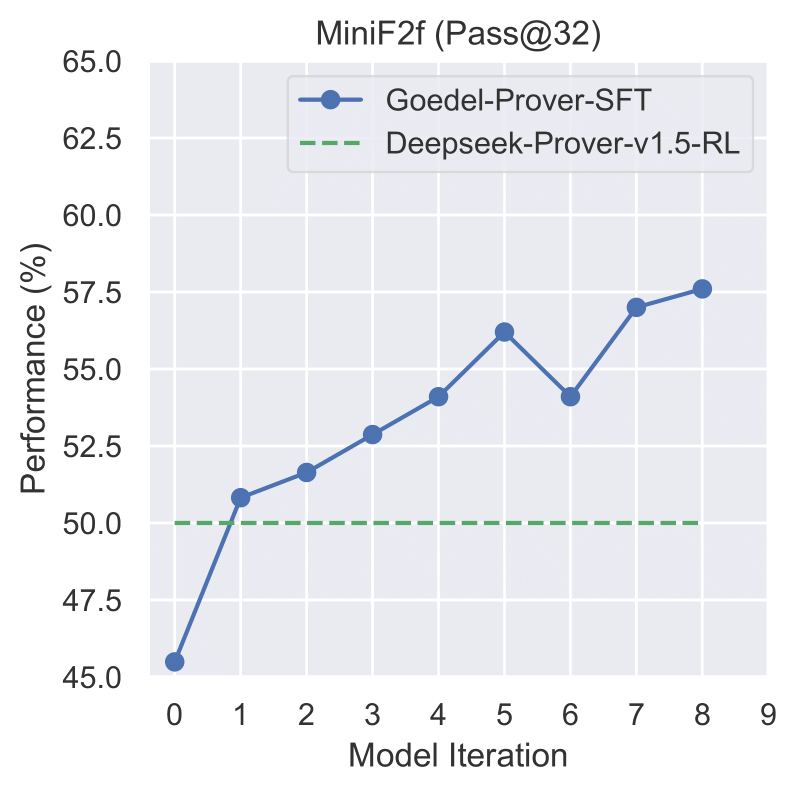
Performance on miniF2F and Held-out datasets
Figure 1: Iterative Performance on miniF2F
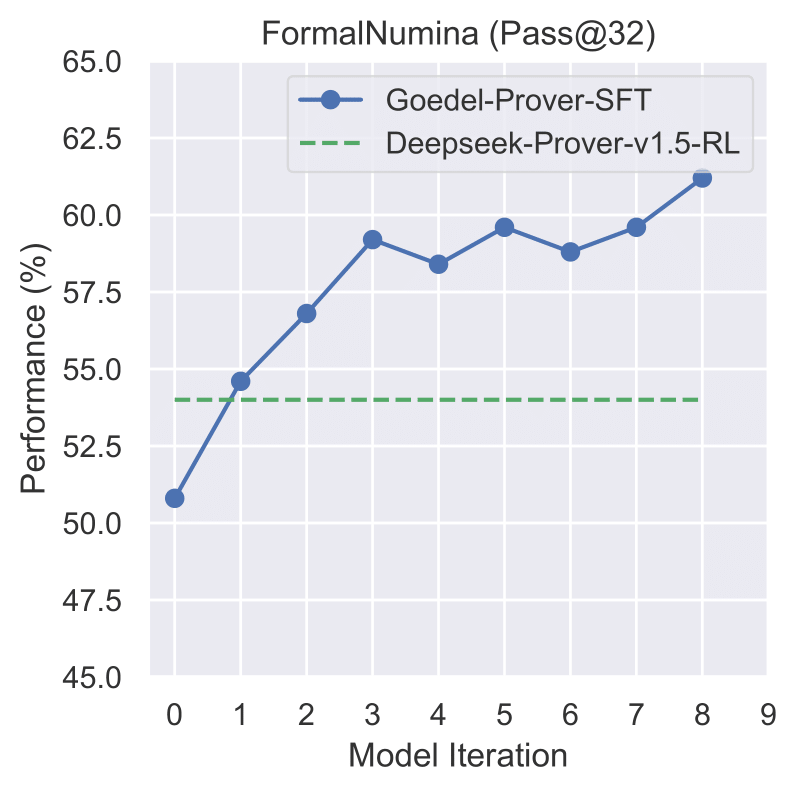
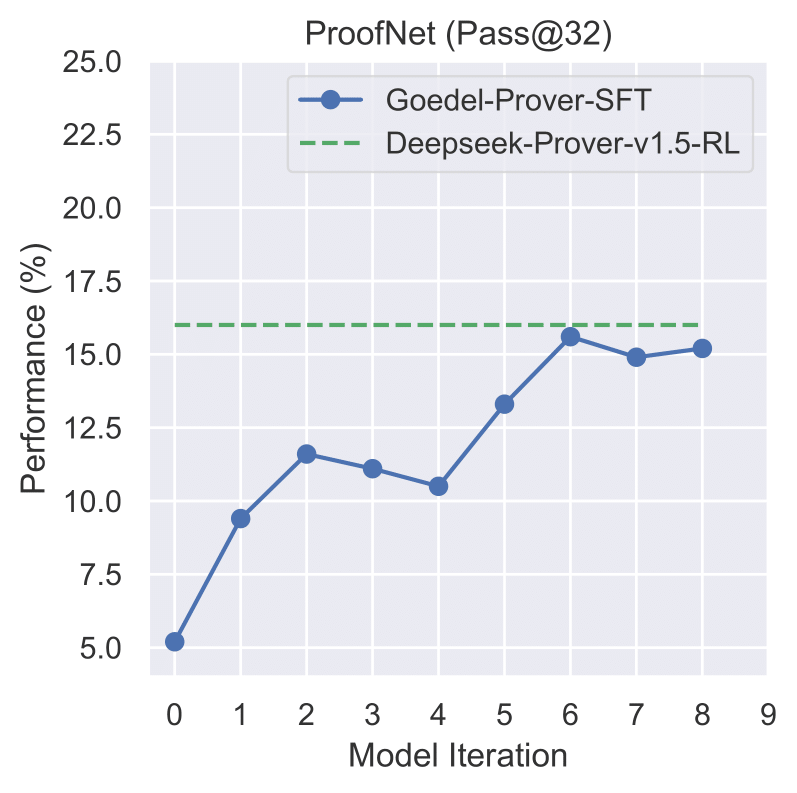
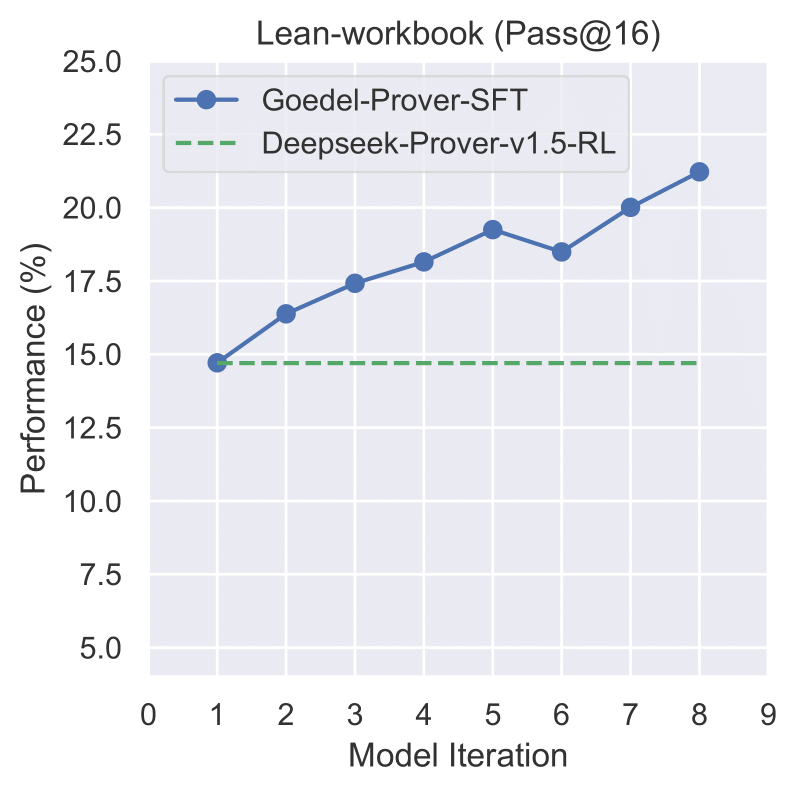
Performance on ProofNet and Lean-workbook
Figure 2: Iterative Performance on FormalNumina
Performance on ProofNet and Lean-workbook
Figure 3: Iterative Performance on ProofNet
Performance on ProofNet and Lean-workbook
Figure 4: Iterative Performance on Lean-workbook

The performance trends illustrated in Figures 1-4 demonstrate the consistent improvement of our model across different datasets during the iterative training process.

Key Findings

  • Achieving state-of-the-art performance of 57.6% on miniF2F at Pass@32
  • Ranking the 1st on the PutnamBench Leaderboard with 7 problems solved out of 644 with Pass@512
  • Cumulatively solving 29.7K problems in Lean-workbook. We significantly increase the 15.7K proofs found by prior works.
  • Iterative training process demonstrates consistent improvement in model performance

BibTeX


        @misc{lin2025goedelproverfrontiermodelopensource,
          title={Goedel-Prover: A Frontier Model for Open-Source Automated Theorem Proving}, 
          author={Yong Lin and Shange Tang and Bohan Lyu and Jiayun Wu and Hongzhou Lin and Kaiyu Yang and Jia Li and Mengzhou Xia and Danqi Chen and Sanjeev Arora and Chi Jin},
          year={2025},
          eprint={2502.07640},
          archivePrefix={arXiv},
          primaryClass={cs.LG},
          url={https://arxiv.org/abs/2502.07640}, 
        }